Question

The height in feet (h) of the ball t seconds after it is released can be modeled using the formula:-16t² + 10t+ 6 = hFind the time, in seconds, passed before the ball hits the ground (let h = 0).*

Answer 1

As the problem suggests, we must do h = 0, then we must solve the following quadratic equation

`-16t^2+10t+6=0`

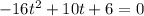
We can simplify it to (divide all terms by 2)

`-8t^2+5t+3=0`

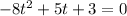
Now we can use the quadratic formula to solve it

`\begin{gathered} t=(-b \pm√(b^2 - 4ac))/(2a) \\ \\ \end{gathered}`

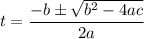
Where

a = -8

b = 5

c = 3

Then

`\begin{gathered} t=(-5\pm√(5^2-4\cdot(-8)\cdot3))/(2\cdot(-8)) \\ \\ t=(-5\pm√(25+96))/(-16) \\ \\ t=(5\pm√(121))/(16) \\ \\ t=(5\pm11)/(16) \\ \end{gathered}`

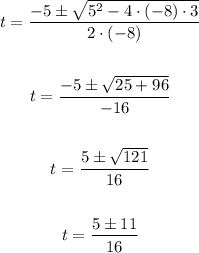
Therefore the solutions are

`\begin{gathered} t=(5+11)/(16)=1 \\ \\ t=((5-11))/(16)=(-6)/(16)=-(3)/(8) \end{gathered}`

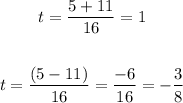
The only valid solution is t = 1, because we can have negative time, therefore the answer is t = 1

Final answer: