Notice that the first two terms of the expression have x² as a common factor, and the last two terms have 36 as a common factor.
Factor out x² from the first two terms, and -36 from the last two terms:
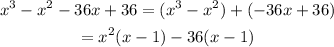
Now, we are left with two terms that have (x-1) as a common factor. Factor out (x-1) from the expression:
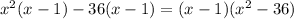
Notice that 36 is equal to 6². Rewrite the expression using this fact:
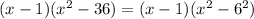
The second factor of the expression is a difference of squares. Remember that a difference of squares can be factored out as the product of two conjugate binomials, as follows:
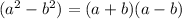
Then, factor out the difference of squares x²-6² as a product of two conjugate binomials. Be careful to place the minus sign correctly:
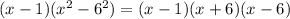
Then, the complete factorization of the polynomial is:
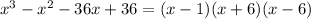
To solve the equation, remember that any expression multiplied by 0 is equal to 0. So, if the product of three factors is equal to 0, there are three possibilities, since the whole expression will be equal to 0 whenever any of the factors is equal to 0:

Therefore, the solution set for this equation is {-6,1,6}. The complete factorization of the given polinomial is (x-1)(x+6)(x-6).