So,
We could draw the situation here below:
Remember that sin(θ) is a relation between the opposite side of the angle θ, and the hypotenuse of the right triangle.
In this case, we could write that:
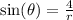
But, using the pythagorean theorem, we could find the value of r:
![\begin{gathered} r=\sqrt[]{3^2+4^2} \\ r=\sqrt[]{25} \\ r=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lwce4daz9s3nd1seywb8p8ptoigte2s03g.png)
Then,
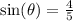
Now, we're asked to find the value of sin(2θ). To do this, we could use the fact that:

So, we would need to know the value of cos(θ), which is the ratio between the adjacent side of the angle θ and the hypotenuse r. This is,
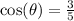
Now, we could replace these values in the expression given, to obtain:
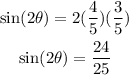
Therefore, sin(2θ) = 24/25