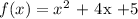
Step 1:
To get the vertex
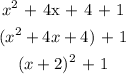
Comparing this to the equation in the vertex form
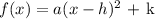
-h = 2
h= -2
k =1
So the vertex is (h,k) = (-2, 1)
The axis of symmetry is at -2
The minimum value can be obtained from the equation
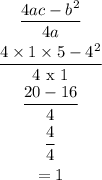
The vertex is (-2, 1)
The axis of symmetry is at -2
The minimum value is 1 ( i.e coordinate (-2,1)