ANSWER
9 years
Step-by-step explanation
As we can see in the equation, the initial deposition is 1000. We want to find in how many years the account balance will double, in other words, we have to find t for f(t) = 2000,
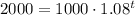
First, we have to divide both sides of the equation by 1000,
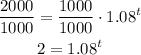
To be able to solve for t, we have to apply a logarithm to both sides of the equation, so we can use the property of exponents,
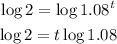
Finally, divide both sides by log(1.08) and solve,
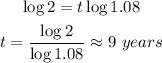
It will take about 9 years for the account balance to double,