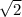Question

assume angle c is a right angle and given the conditions ________ solve for the side lengths of the right angle. i’ve attached an image

Answer 1

Given:

In triangle ABC,

The angle C is a right angle.

`\begin{gathered} \angle B=45^(\circ) \\ c=2 \end{gathered}`

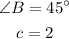
To solve:

The triangle

Step-by-step explanation:

Since the given triangle has an angle of 45 degrees.

So, it is an isosceles right triangle.

By Pythagoras theorem,

`\begin{gathered} a^2+b^2=c^2 \\ a^2+a^2=2^2 \\ 2a^2=4 \\ a^2=2 \\ a=√(2) \\ \therefore b=√(2) \end{gathered}`

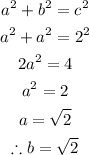
Thus, the length of the other two sides are

`a=√(2),b=√(2)`

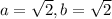
Final answer:

The other side lengths of the triangle are both equal to,

`√(2)`