Question

A loud speaker has an output of 78 dB. If the volume of the sound is turned up so that the output intensity is 1000 times greater, what is the new sound intensity level? answer in:____dB

Answer 1

108 dB

Step-by-step explanation

The speaker has an output sound intensity level of 78 dB. Then, the sound is turned up so that the output intensity is 1000 times greater. We have to find what is the new sound intensity level.

The sound intensity level is given by,

`\beta(dB)=10\log\left((I)/(I_0)\right)`

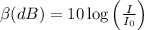
Where I is the intensity of the sound, β is the sound intensity level and I₀ is the hearing threshold of 10⁻¹² W/m².

First, we have to find what is the sound intensity for a sound intensity level of 78 dB. Solving the equation above for I,

`I=I_0\cdot10^(\beta/10)`

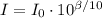
So the intensity for a sound intensity of 78 dB is,

`I=10^(-12)W/m^2\cdot10^(78dB/10)=6.31\cdot10^(-5)W/m^2`

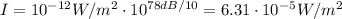
If now the volume is turned up so that this intensity is 1000 times greater, we have that the sound intensity level is,

`\beta=10\cdot\log\left((1000\cdot6.31\cdot10^(-5)W/m^2)/(1\cdot10^(-12)W/m^2)\right)=10\cdot10.8=108dB`

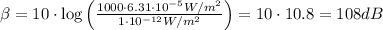
Hence, the new sound intensity level is 108 dB.