The new boiling point is found essentially the same way as the freezing point, except replacing the freezing point quantities with boiling point quantities:

Where,
DeltaTb, is the change in boiling point temperature
Kb, is the molal boiling point
m, is the molality
We have to calculate first which is the molality of the solution.
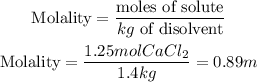
Now, we replace the know data into the first equation:
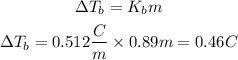
The boiling point of a solution will be the boiling temperature of water alone plus the temperature delta found:
Tb=100°C + 0.46°C=100.46°C
The boiling point of the solution will be 100.46°C