Question

A 456 kg water balloon is dropped from room 209 onto some unsuspecting students (it couldhappen!). If the window of 209 is 8.5 m off the ground, how much kinetic energy does theballoon have right before it hits the ground? What is the final velocity of the balloon right beforeimpact?

Answer 1

We are given that a ball is dropped from a height 8.5 meters and we are asked to determine the kinetic energy. To do that we will use the principle of conservation of energy.

We will consider two points. The first point is when the balloon is on top of the 8.5 meters height and the second point is when the balloon is about to hit the floor. As shown in the diagram:

As we can see in the diagram, At the beginning we have potential energy, but all that potential energy is transformed into kinetic energy, by the time we get to point 2 all that potential energy has been transformed into kinetic energy., since energy must be conserved we have:

`E_1=E_2`

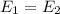
The potential energy is given by:

`E_1=\text{mgh}`

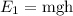
Where:

`\begin{gathered} m=\text{ mass} \\ g=\text{ acceleration of gravity} \\ h=\text{ height} \end{gathered}`

And the kinetic energy is given by:

`E_2=(1)/(2)mv^2`

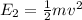
Where:

`v=\text{ velocity}`

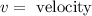
Substituting in the equation we get:

`\text{mgh}=(1)/(2)mv^2`

Since the kinetic energy is equal to the potential energy in this case, then the kinetic energy can be determined as:

`(1)/(2)mv^2=\text{mgh}`

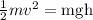
Substituting in the equation we get:

Solving the operations we get:

`(1)/(2)mv^2=37984.8J`

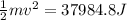
Therefore, the kinetic energy is 37984.8J

Now, to determine the velocity we go back to the conservation of energy equation:

`(1)/(2)mv^2=\text{mgh}`

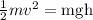
Here, we can cancel out the mass:

`(1)/(2)v^2=gh`

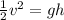
Now we solve for "v" first by multiplying both sides by 2:

`v^2=2gh`

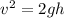
Now we take the square root to both sides:

`v=\sqrt[]{2gh}`

Now we substitute the values:

`v=\sqrt[]{2(9.8(m)/(s^2))(8.5m)}`

Solving the operations:

`v=12.9(m)/(s)`

Therefore, the velocity at the end is 12.9 meters per second.