Question

I got this practice problem with a memorandum answers but I got most of the questions wrong... So I'm just here for solutions since I don't have solutions on how to solve this.. Please be clear as I'm tend to be slow

Answer 1

Given data:

* The equation of the position is,

`x=12\cos (6\pi t+(\pi)/(6))`

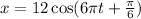
Solution:

(1). From the given equation of the position, the amplitude of the displacement is,

`x_o=12\text{ m}`

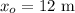
Thus, the amplitude of the oscillation is 12 meter.

(2). The angular frequency of the oscillation from the given equation is,

`\begin{gathered} \omega=6\pi\text{ } \\ \omega=18.85\text{ rad/s} \end{gathered}`

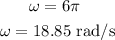
Thus, the angular frequency of the oscillation is 18.85 radian per second.

(3). The linear frequency of the oscillation is,

`\begin{gathered} f=(2\pi)/(\omega) \\ f=(2\pi)/(6\pi) \\ f=(1)/(3) \\ f=0.33\text{ Hz} \end{gathered}`

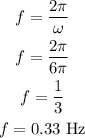
Thus, the frequency of the oscillation is 0.33 Hz.

(4). The time period of oscillation is,

`\begin{gathered} T=(1)/(f) \\ T=(1)/(0.33) \\ T=3\text{ s} \end{gathered}`

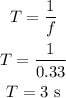
Thus, the time period of the oscillation is 3 seconds.

(5). The position of the oscillator at tiem t = 0 s is,

`\begin{gathered} x=12\cos (6\pi*0+(\pi)/(6)) \\ x=12\text{cos(}(\pi)/(6)\text{)} \\ x=11.99 \\ x\approx12\text{ m} \end{gathered}`

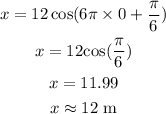
Thus, the position of the oscillator at time t=0 seconds is 12 meter.

(6). The maximum speed of the oscillator is,

`\begin{gathered} v=x_o\omega \\ v=12*18.85 \\ v=226.2\text{ m/s} \end{gathered}`

Thus, the maximum value of velocity is 226.2 m/s.

(7). The maximum acceleration of the oscillator is,

`\begin{gathered} a=\omega^2x_o \\ a=(18.85)^2*12 \\ a=4263.9ms^(-2) \end{gathered}`

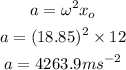
Thus, the maximum acceleration of the oscillator is 4263.9 meter per second squared.

(8). The displacement of the oscillator at the 5 second is,

`\begin{gathered} x=12\cos (6\pi t+(\pi)/(6)) \\ x=12\cos (6\pi*5+(\pi)/(6)) \\ x=-0.998 \\ x\approx-1\text{ m} \end{gathered}`

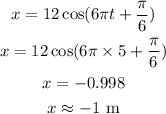
Thus, the displacement of oscillator after 5 seconds is -1 meter.

(9). The velocity of the oscillator in terms of time is,

`\begin{gathered} v=(dx)/(dt) \\ v=(d)/(dt)(12\cos (6\pi t+(\pi)/(6))) \\ v=12*6\pi*-\sin (6\pi t+(\pi)/(6)) \\ v=-72\pi\sin (6\pi t+(\pi)/(6)) \end{gathered}`

The velocity of the oscillator at time 5 seconds is,

`\begin{gathered} v=-72\pi\sin (6\pi*5+(\pi)/(6)) \\ v=-225.4\text{ m/s} \end{gathered}`

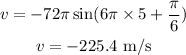
Thus, the velocity of the oscillator at 5 seconds is -225.4 meter per second.

(10). The acceleration of the oscillator is,

`\begin{gathered} a=(dv)/(dt) \\ a=(d)/(dt)(-72\pi\sin (6\pi t+(6)/(\pi))) \\ a=-72\pi*6\pi\cos (6\pi t+(6)/(\pi)) \end{gathered}`

The value of acceeration at tiem 5 seconds is,

`\begin{gathered} a=-72\pi*6\pi\cos (6\pi*5+(6)/(\pi)) \\ a=354.65ms^(-2) \end{gathered}`

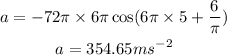
Thus, the acceleration of the oscillator at 5 second is 354.65 meter per second squared.