Question

Hello I really need help solving this practice from my trig prep book

Answer 1

From the statement, we know that:

`\begin{gathered} \cos \theta=-\frac{\sqrt[]{2}}{3},\text{ where }\pi\leq\theta\leq(3)/(2)\pi, \\ \tan \beta=(4)/(3),\text{ where 0}\leq\theta\leq(\pi)/(2)\text{.} \end{gathered}`

1) First, we look for the value of angle θ.

Plotting both sides of the equation, we have the graph:

Using a calculator, we get the following value of θ:

`\theta^(\prime)=\arccos (-\frac{\sqrt[]{2}}{3})\cong2.06.`

But to get an angle in the interval π ≤ θ ≤3π/2, the correct result is:

`\theta=2\pi-\theta^(\prime)\cong4.22.`

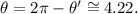
We can check this result from the graph above.

The of θ is:

`\sin (\theta)=-\frac{\sqrt[]{7}}{3}\text{.}`

2) Secondly, we look for the value of angle β.

Using a calculator, we get the following value of β:

`\beta=\arctan ((4)/(3))\cong0.93.`

This result is in interval 0 ≤ θ ≤ π/2.

The sine and cosine of β are:

`\begin{gathered} \sin \beta=(4)/(5), \\ \cos \beta=(3)/(5). \end{gathered}`

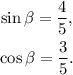
3) Using the results above, the sine of the sum of the angles θ and β is:

`\sin (\theta+\beta)=\sin \theta\cdot\cos \beta+\sin \beta\cdot\cos \theta\text{.}`

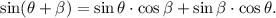
Replacing the values obtained above, we get:

`\sin (\theta+\beta)=(-\frac{\sqrt[]{7}}{3})\cdot(3)/(5)+(4)/(5)\cdot(-\frac{\sqrt[]{2}}{3})=-\frac{\sqrt[]{7}}{5}-\frac{4\cdot\sqrt[]{2}}{15}\text{.}`

Answer

`\sin (\theta+\beta)=-\frac{\sqrt[]{7}}{5}-\frac{4\cdot\sqrt[]{2}}{15}`