The exponential function
The general form of the exponential function is:
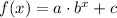
Where b is the ratio of growth or decay of the function.
The function can be identified as a growing or decaying trend according to:
* If b is greater than 1, the function is growing
* If b is less than 1, the function is decaying.
Now let's analyze the given functions:
A)
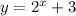
The ratio of this function is b=2, thus the function is growth.
B)
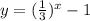
Here, the value of b is 1/3 and it's less than 1, thus the function is decay.
C)
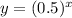
Here, the value of b is 0.5 and it's less than 1, thus the function is decay
Answer:
A) Growth
B) Decay
C) Decay