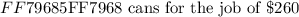Question

Max is earning extra money by painting houses. He charges a $200 fee plus $12 per can of paint needed to complete the job. find how many cans of paint he needs to an $260 job.

Answer 1

Max earns a few extra bucks by painting houses. He charges his customers using the following rates:

`\begin{gathered} \text{Base Job Fee = \$200} \\ \text{Rate =\$}(12)/(can) \end{gathered}`

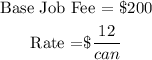
Max charges a basic job fee and a rate to the number of cans of paint required for the completion of job.

We will denote the number of cans of paint required to complete a job as:

`\text{Number of cans required = x}`

Lets assume Max gets some paint job. Over the job he used ( x ) number of cans to complete. At the end of the job he charges a receipt to the customer. He will formulate the following relation to charge the customer:

`\begin{gathered} \text{Total receipts = Base Job Fee + Rate}\cdot x \\ \text{\textcolor{#FF7968}{Total receipts = \$200 + \$}}\textcolor{#FF7968}{(12)/(can)\cdot x} \end{gathered}`

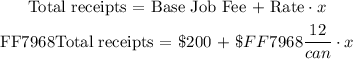
We will use the above expression to evaluate the number of cans Max needs to complete a job for a receipt off ( $260 ):

`\begin{gathered} \text{ \$260 = \$200 + \$}(12)/(can)\cdot x \\ 60\text{ = }(12)/(can)\cdot x \\ x\text{ = }(60)/(12) \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 5 cans}} \end{gathered}`

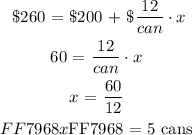
Max will require:

`\textcolor{#FF7968}{5}\text{\textcolor{#FF7968}{ cans}}\text{ for the job of \$260}`