We know that Gilbert's first practice ride covers 5 miles of the course, and his second practice ride covers 9 miles of the course.
And we also know that between these practice rides, he increase his average speed by 2 miles/hour.
We have the next two functions:
- First practice ride :
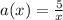
- Second practice ride :
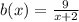
Where, x represents his speed during the first practice ride
a) We know that
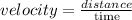
So, if the functions model the time
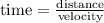
We can see that the denominator represents the velocity.
Finally, the denominator of the function that models practice ride 2 represent the biking speed for the second practice ride.
b) Knowing that a(x) and b(x) represent the time it took Gilbert to do each practice ride,
to find the a function that models the total amount of time Gilbert spent doing practice rides on the race course, add the functions.