Question

The dollar value of a car is a function f, . of the number of years, t, since the car was purchased. Thefunction is defined by the equations f(t) = 12000*(3/5)^ta. What does the 12,000 tell us about the situationb. What does the 3/5tell us about the situation?C.What will be the value of the car after 3 years?

Answer 1

Given the following question:

`f(t)=12000*((3)/(5))^t`

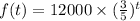
Part A:

I believe that the 12,000 tells us the orginal price of the car, or the price the car was purchased for. 12000 is the orginal price of the car.

Part B:

I believe that the 3/5 tells us the decline in value each year after the car has been purchased. Which is why t is the exponet is t was 2 you would have to multiply 3/5 by itself twice and then multiply it by 12000 which further decreases it's value. 3/5 represents the decline in value after T years.

Part C:

t = number of years

t = 3

`\begin{gathered} f(t)=12000*\frac{3}{5^{}}^3 \\ (3)/(5)^3=(3)/(5)*(3)/(5)*(3)/(5) \\ (3)/(5)*(3)/(5)=(9)/(25) \\ (9)/(25)*(3)/(5)=(27)/(125) \\ 12000*(27)/(125)=2592 \\ v=2592 \end{gathered}`

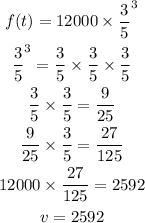
Value of the car after three years will be 2592.