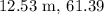Question

elasieL. 111, 10.07 g8. Given the vectors A = 6 m west and B = 11 m south, using graphicalmethod determine which of the following most likely representthe magnitude and direction of the difference vector A - B respectively.(You should be able to answer it with sketches not drawn to scale.) (1 point)A. O 12.53 m, 61.39 degB. O 12.53 m, 118.61 degC. O 12.53 m, 241.39 degD. O17 m, 118.61 degE. O 17 m, 61.39 deg

Answer 1

Given:

The vectors are,

`\begin{gathered} \vec{A}=6\text{ m west} \\ \vec{B}=11\text{ m south} \end{gathered}`

To find:

The subtraction,

`\vec{A}-\vec{B}`

using graphical method

Step-by-step explanation:

The representation of the vectors is shown below:

We can write,

`\begin{gathered} \vec{A}-\vec{B} \\ =\vec{A}+(-\vec{B}) \end{gathered}`

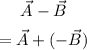
This is represented in the image above.

The magnitude of the resultant is,

`\begin{gathered} \lvert{\vec{A}-\vec{B}}\rvert=√(A^2+(-B)^2) \\ =√(6^2+(-11)^2) \\ =√(36+121) \\ =√(157) \\ =12.53\text{ m} \end{gathered}`

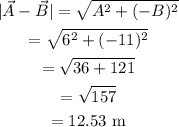
The angle with the east is,

`\begin{gathered} \theta=tan^(-1)(11)/(6) \\ =61.39\degree \end{gathered}`

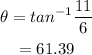
Hence, the resultant vector's magnitude and the direction are,

`12.53\text{ m, 61.39}\degree`