Question

The table and scatter plot show the number of hours worked, x, and the amount of money spent on entertainment, y, by each of 9 students.The equation of the line of best fit is y = 0.9x + 18.56

Answer 1

Given the table below:

whose line of best fit is expressed as

`y=0.9x+18.56`

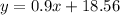
The observed amount spent on entertainment is the value of y for a corresponding value of x in the table of value.

The predicted amount spent on entertainment is the value of y for a corresponding value of x in the equation of line of best fit.

The residual is the difference between the observed amount and predicted amount spent on entertainment.

Thus, given:

`\begin{gathered} When\text{ x=7.9,} \\ Observed\text{ amount spent on entertainment \lparen in dollars\rparen=28.50} \\ Predicted\text{ amount spent on entertainment=0.9\lparen7.9\rparen+18.56} \\ =25.67 \\ Residual(in\text{ dollars\rparen =28.50-25.67} \\ =2.83 \end{gathered}`
`\begin{gathered} when\text{ x=12.0,} \\ Observed\text{ amount spent on entertainment \lparen in dollars\rparen=29.36} \\ Predicted\text{ amount spent on entertainment \lparen in dollars\rparen=0.9\lparen12.0\rparen+18.56} \\ =29.36 \\ Residual\text{ \lparen in dollars\rparen=29.36-29.36} \\ =0 \end{gathered}`

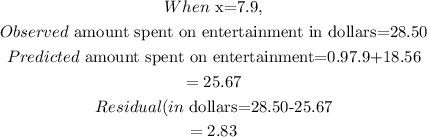
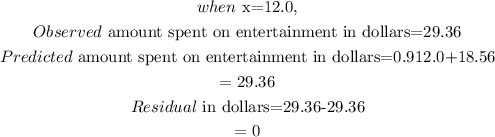
Hence,