Question

I need help with x^2+10=7x

Answer 1

The given expression : x^2+10=7x​

`x^2+10=7x`

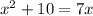
Simplify and factorize:

`\begin{gathered} x^2+10=7x \\ x^2-7x+10=0 \end{gathered}`

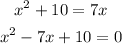
Expand the number (-7) such that when we add or subtract the numbers we get (-7) and when multiply we get 10

So, (-5) + (-2) = (-7), (-5) x (-2) = 10

expression can be written as:

`\begin{gathered} x^2-7x+10=0 \\ x^2-5x-2x+10=0 \end{gathered}`

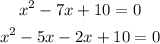
Now take x common from the first two parts and -2 from last two parts:

`\begin{gathered} x^2-5x-2x+10=0 \\ x(x-5)-2(x-5)=0 \end{gathered}`

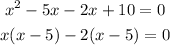
Now take (x-5) Common:

`\begin{gathered} x(x-5)-2(x-5)=0 \\ (x-5)(x-2)=0 \end{gathered}`

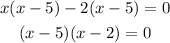
To get the value of x, compute each factor with zero:

`\begin{gathered} (x-5)=0 \\ x=5 \\ (x-2)=0 \\ x=2 \end{gathered}`

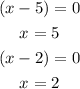
So, the value of x are :

x =2, x = 5

Answer : x =2, x = 5