The function given in the question is
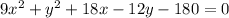
Rearrange the function above connecting similar terms

Factorize the equation in brackets

Solve the brackets using completing the square method but multiplying the coefficient of x and y by 1/2 and then square

By simplifying the equation above, we will have

Divide all through by 225

The general formula for the equation of an ellipse is
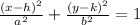
Where the center of the ellipse is
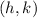
By comparing coefficients, we will have that
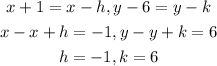
The centre of the ellipse is
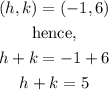
Therefore,
The value of h+k = 5