Question

Square the binomial using Binomial Squares Pattern (simplify) (w + 4)^2

Answer 1

Hello!

We have the binomial below:

`\mleft(w+4\mright)^2`

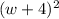
First, notice that we have two terms inside the square, right?

• w ,= first term

,

• 4 ,= second term

To solve it using the Binomial Square Pattern, we will have to follow some steps:

0. Square the first term

,

1. Multiply the first by the second term, then multiply it by 2

,

2. Square the second term

,

3. Sum all steps above.

Let me explain step by step now:

1)

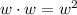
`w\cdot w=w^2`

2)

`(w\cdot4)\cdot2=4w\cdot2=8w`

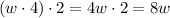
3)

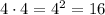
`4\cdot4=4^2=16`

4)

`(w+4)^2=w^2+8w+16`

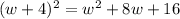
So, your answer will be:

w² +8w +16