Given the equation of the revenue R:
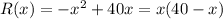
We know that by charging x dollars for a certain computer, the owner can sell 40-x computers each week. Then, if x is the charge for a certain computer, the revenue is given by the product of the number of computers he sells and the charge of that computer.
The equation of the revenue received when the selling price of a computer is $x. To find the maximum revenue, we find the vertex form of the quadratic equation of the revenue. By completing squares:
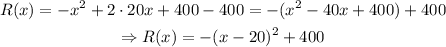
Then, the maximum revenue is the y-coordinate of the vertex, that is:
![undefined]()