Question

Hello, May I please request if you can go over number#13?Thank you

Answer 1

In this problem, we are trying to find the vertex of the quadratic function. There are two ways to do this (using the axis of symmetry or completing the square).

Let's start with the "easier" method: using the axis of symmetry.

First, we will find the axis of symmetry using a special formula. Then we substitute that value into the original function to get the vertex.

The axis of symmetry will represent the x-value of the vertex, and the f(x) value will represent the y-value of the vertex.

Axis of Symmetry Equation

`x=-(b)/(2a)`

The given function is in standard form:

`\begin{gathered} f(x)=ax^2+bx+c \\ \\ f(x)=2x^2-8x+3 \end{gathered}`

Notice the b-value is -8, and the a-value is 2. We will substitute these into the axis of symmetry formula to find the y-value:

`x=-((-8))/(2(2))=(8)/(4)=2`

So, the x-value of the vertex is 2. Now, let's find the y-value.

`\begin{gathered} x=2 \\ \\ f(2)=2(2)^2-8(2)+3=8-16+3=-5 \end{gathered}`

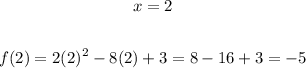
The y-value of the vertex is -5.

So, the vertex is (2,-5).

An additional method is to use completing the square. This is often used with solving quadratic equations and rewriting conic equations.

We begin with the original function:

`f(x)=2x^2-8x+3`

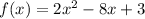
Subtract 3 from both sides so that we can complete the square on the right-hand side:

`f(x)-3=2x^2-8x`

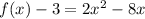
To complete the square, the a-value must be 1, so next we can divide each side by 2:

`(f(x)-3)/(2)=x^2-4x`

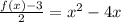
The left-hand side will begin to look messy, so don't try to simplify anything on that side.

To complete the square, we will divide by b-value by 2, then square it.:

`((-4)/(2))^2=(-2)^2=4`

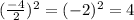
Add that new square (4) to both sides:

`(f(x)-3)/(2)+4=x^2-4x+4`

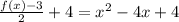
Now, the right hand side is a perfect square trinomial that can be factored:

`(f(x)-3)/(2)+4=(x-2)^2`

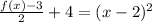
All the extra "stuff" that we did on the left-hand side can now be undone to isolate f(x) again. Subtract 4 from both sides:

`(f(x)-3)/(2)=(x-2)^2-4`

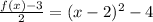
Multiply by 2:

`f(x)-3=2(x-2)^2-8`

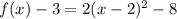
Add 3:

`f(x)=2(x-2)^2-5`

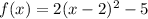
Now the function is in vertex form! So we see that the vertex is (2,-5).