Given:
The cannonball is launched at an angle of: θ = 35°
The initial velocity of the cannonball is: u = 36 m/s
To find:
The time of flight of the cannonball and the range (horizontal distance it traveled)
Step-by-step explanation:
The time of flight of the cannonball is calculated as:
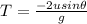
The negative sign in the above equation indicates that the direction of the verticle velocity of the cannonball is opposite to acceleration due to gravity.
Substituting the values in the above equation, we get:
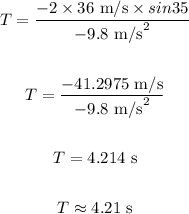
Now, the horizontal distance covered by the cannonball is calculated as:
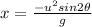
Substituting the values in the above equation, we get:
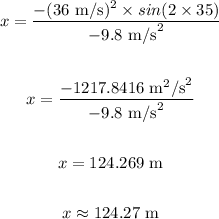
Final answer:
The cannonball spends 4.21 seconds of time in the air.
The horizontal distance traveled by the cannonball is 124.27 meters.