Question

Rotate XYZ 90° clockwise around the origin to form X'Y'Z'. Then dilate the image by a scale factor 1/2 of with the center of dilation at the origin to form X”Y”Z”.

Answer 1

We have to apply this two transformations:

1) rotation 90° CW around the origin.

2) dilate the image by a scale factor of 1/2 with center of dilation in the origin.

We can draw the first transformation for a generic point (x,y) and find the rule:

Then, we can write the rule as:

`P=(x,y)\longrightarrow P^(\prime)=(y,-x)`

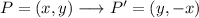
Now, we can write the rule for the dilation as:

`P^(\prime)=(y,-x)\longrightarrow P^(\prime\prime)=(k\cdot y,-k\cdot x)=((1)/(2)y,-(1)/(2)x)`

We then will calculate each of the transformation for each of the points, applying the rules we have written:

`P=(x,y)\longrightarrow P^(\prime)=(y,-x)\longrightarrow P^(\prime)^(\prime)=((1)/(2)y,-(1)/(2)x)`

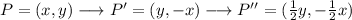
For each of the points we will get:

`X=(-2,2)\longrightarrow X^(\prime)=(2,-(-2))=(2,2)\longrightarrow X^(\prime\prime)=((1)/(2)\cdot2,(1)/(2)\cdot2)=(1,1)`
`Y=(-4,2)\longrightarrow Y^(\prime)=(2,4)\longrightarrow Y^(\prime)^(\prime)=(1,2)`
`Z=(-2,6)\longrightarrow Z^(\prime)=(6,2)\longrightarrow Z^(\prime)^(\prime)=(3,1)`

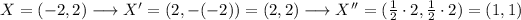
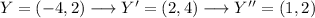
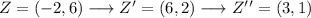
We can graph the points to see if the transformations are well done:

Answer:

X'Y'Z':

X'=(2,2)

Y'=(2,4)

Z'=(6,2)

X"Y"Z":

X''=(1,1)

Y''=(1,2)

Z''=(3,1)