Step 1: Write out the terms in the question
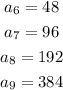
Step 2: Find the common ratio ( r )
The ratio between two consecutive terms gives the common ratio
That is,
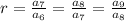
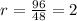
Step 3: Find the first term by substituting the value of r
Firstly, write out the general term of a geometric progression
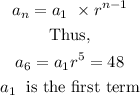
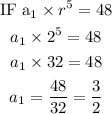
Thus, the first term is 3/2