Question

The field inside a running track is made up of arectangle that is 84.39 m long and 73 m wide, together with a half-circle at each endThe track is 9.76 m wide all the way around. What is the distance around the outside of the track?Exact answer.

Answer 1

(168.78 + 92.52π) m

Step-by-step explanation:

The distance around the outside of the track is equal to two times the length of the rectangle added to the distance of two semi-circles.

So, two times the length of the rectangle is equal to

2 x 84.39 m = 168.78 m

On the other hand, the two semicircles form one circle and its perimeter is equal to

`C=\pi d`

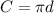
Where d is the diameter of the semicircles. Taking into account the figure, the diameter is the width of the rectangle added to two times the width of the track, so

d = 73 m + 2(9.76m)

d = 73 m + 19.52 m

d = 92.52 m

Then the perimeter of the circle is

`C=\pi(92.52m)=92.52\pi\text{ m}`

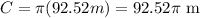
Now, the total distance around the inside of the track is

168.78 m + 92.52π m = (168.78 + 92.52π) m