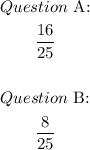Solution
- The information given to us can be written mathematically as:
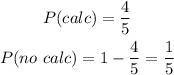
Question A:
- If two students are chosen at random and both of them have a calculator, this means that the probability of choosing the two of them is calculated by the AND formula.
- That is,

Question B:
- The probability that only one of them has a calculator implies that 1 has a calculator and the other does not have a calculator.
- Thus, we have:

Final Answer
The answers are: