Question

11. What is the solution of matrix equation«[?]* =][17]X =- [27]x- -17)Ox=17=

Answer 1

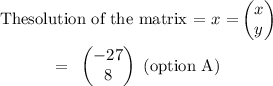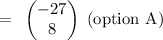
`=\text{ }\begin{pmatrix}-27 \\ 8\end{pmatrix}\text{ (option A)}`Step-by-step explanation:
`\begin{gathered} \\ \begin{pmatrix}1 & 7 \\ 3 & 4\end{pmatrix}\text{ }*\text{ x = }\begin{pmatrix}2 \\ 5\end{pmatrix} \end{gathered}`
`\begin{gathered} \text{let x =}\begin{pmatrix}x \\ y\end{pmatrix} \\ \begin{pmatrix}2 & 7 \\ 1 & 4\end{pmatrix}\text{ }*\begin{pmatrix}x \\ y\end{pmatrix}\text{ = }\begin{pmatrix}2 \\ 5\end{pmatrix} \\ mu\text{ltiplying the matrix:} \\ 2(x)\text{ + 7(y) = 2} \\ 2x\text{ + 7y = 2 }\ldots equation1 \\ 1(x)\text{ + 4(y) = 5} \\ x\text{ + 4y = 5 }\ldots equation2 \end{gathered}`

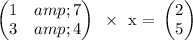
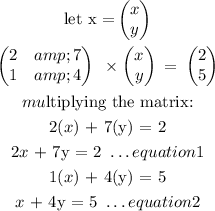
Using elimination method:

multiply equation 2 by 2

2(x) + 2(4y) = 2(5)

2x + 8y = 10 ...equation 2

combine both equations:

2x + 7y = 2 ...equation 1

2x + 8y = 10 ...equation 2

subtract equation 2 from 1:

2x - 2x + 7y - 8y = 2 - 10

0 - y = -8

-y = -8

y = -8/-1

y = 8

substitute for y in equation 2:

x + 4y = 5

x + 4(8) = 5

x + 32 = 5

x = 5 - 32

x = -27

`\begin{gathered} \text{Thesolution of the matrix = }x\text{ =}\begin{pmatrix}x \\ y\end{pmatrix} \\ =\text{ }\begin{pmatrix}-27 \\ 8\end{pmatrix}\text{ (option A)} \end{gathered}`