Answer : x = 4 and y = 1
We are given the below system of equations
-3x + 4y = -8
-3x + 2y = -10
This system of equations can be solve using elimination method
To use elimination method, we need to eliminate one of the variables
-3x + 4y = -8 -------------- equation 1
-3x + 2y = -10 ------------- equation 2
Since, the coefficient of x is the same in both equations, then, we can eliminate the variable x
To eliminate x, substract equation 2 from 1
-3x - (-3x) + 4y - 2y = -8 - (-10)
minus x minus = plus; According to the basic rule of mathematics
-3x + 3x + 4y - 2y = -8 + 10
0 + 2y = 2
2y = 2
Divide both sides by 2
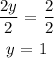
To find x, substitute the value of y = 1 into equation 1
-3x + 4y = -8
-3x + 4(1) = -8
-3x + 4 = -8
Isolate -3x
-3x = -8 - 4
-3x = - 12
Divide both sides by -3
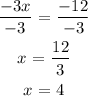
Hence, x = 4 and y = 1: (4, 1)