In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
total marbles = 10
green = 2
red = 2
blue = 4
probability that both marbles he chooses are green = ?
Step 02:
simple probability = favorable outcomes / total outcomes
1st event: probability of green marble
pg1 = 2 / 10
2nd event: probability of green marble
pg2 = 1 / 9
total probability:
total probability = pg1 + pg2
total probability = 2/10 + 1/9
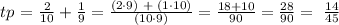
The answer is:
The probability that both marbles he chooses are green is 14 /45