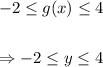Question

Need help with questions 2 and 3 I’m super stuck

Answer 1

B. Domain: all real numbers Range: -2 ≤ y ≤ 4

Step-by-step explanation

The given function is:

`g(x)=3cos(2x+\pi)+1`

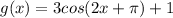
What to find:

The domain and range of the function.

Step-by-step solution:

Domain

Note that the domain of a function is the set of input or argument values for which the function is real and defined.

Therefore, the domain of the function is all real numbers because the function has no undefined points or domain constraints.

Range

Range is a set of values of the independent variable for which a function is defined.

The range of the basic cos function is -1 ≤ cos (2x + π) ≤ 1

-1 ≤ cos (2x + π) ≤ 1

Multiply the edges of the range by 3:

3 (-1) ≤ cos (2x + π) ≤ 3(1) = -3 ≤ cos (2x + π) ≤ 3

Now add 1 to the edges of the range:

1 + (-3) ≤ cos (2x + π) ≤ 1 + 3 = -2 ≤ cos (2x + π) ≤ 4

Therefore, the range of the function is:

`\begin{gathered} -2\leq g(x)\leq4 \\ \\ \Rightarrow-2\leq y\leq4 \end{gathered}`