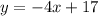To solve the exercise, you can first graph the points to see if they have a linear relationship, that is, if all the points are on the same line. So, you have
Since the relationship of the points is linear, then you can take two of the points through which the line passes, find the slope of the line, and then use the formula point-slope.
The formula for the slope is
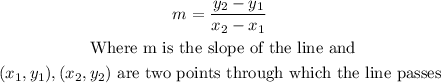
If for example, you take the points
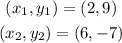
You have
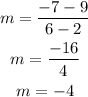
Now using the formula point-slope, that is,

You have
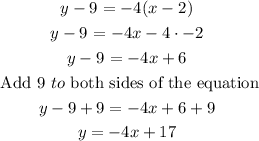
Therefore, the equation representing the values in the table is