Question

Which equation represents the amount inthe account after t years if the interest in compounded daily.

Answer 1

The formula for compound interest is:

`A(t)=P(1+(r)/(n))^(nt)`

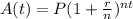
Where:

A is the amount in the account after t years.

P is the amount initially invested.

r is the rate of compounding per year, in decimal.

n is the number of times compounded in a year.

t is the number of years since the initial investment.

The problem tells us:

The initial amount is P = 12000

The annual compounding rate is 4.5%, to convert to decimal, we divide by 100:

`r=(4.5)/(100)=0.045`

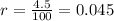
Since the amount is compounded daily, it's compounded 365 times a year. Thus, n = 365

Now we can write:

`A(t)=12000(1+(0.045)/(365))^(365t)`

Which is option 3

Thus, the correct answer is option 3:

`A(t)=12000(1+(0.045)/(365))^(365t)`