Question

Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click on the graph-a-function button

Answer 1

The given equation of the parabola is:

`y=(x+2)^2-3`

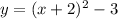
It is required to plot five points: the vertex, two points to the right of the vertex, and two points to the left of the vertex. Then, it is also required to click on the graph-a-function button to graph the parabola.

Recall that the vertex of a parabola whose equation is written in vertex form,

y=(x-h)²+k is given as:

`Vertex=(h,k)`

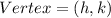
Rewrite the given equation as:

`y=(x-(-2))^2+(-3)`

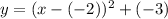
It follows that h=-2 and k=-3.

Hence, the vertex of the parabola is (-2,-3).

Find two points to the left of the vertex.

Substitute x=-3 into the equation:

`\begin{gathered} y=(-3+2)^2-3 \\ \Rightarrow y=(-1)^2-3=1-3=-2 \end{gathered}`

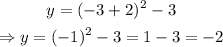
A point is (-3,-2).

Substitute x=-4 into the equation:

`\begin{gathered} y=(-4+2)^2-3 \\ \Rightarrow y=(-2)^2-3 \\ \Rightarrow y=4-3=1 \end{gathered}`

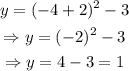
Another point to the left of the vertex is (-4,1).

Find two points to the right of the vertex.

Substitute x=-1 into the equation:

`\begin{gathered} y=(-1+2)^2-3 \\ \Rightarrow y=(1)^2-3=1-3=-2 \end{gathered}`

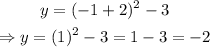
A point to the right is (-1,-2).

Substitute x=0 into the equation:

`\begin{gathered} y=(0+2)^2-3 \\ \Rightarrow y=(2)^2-3=4-3=1 \end{gathered}`

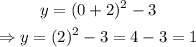
Another point to the right is (0,1).

Plot the points as shown:

Click the graph-a-function button to get the required graph: