Question

Hi can you help me find the answers to each problem? Thanks!

Answer 1

Given:

The function and its point are given.

To match the function with its point:

Step-by-step explanation:

a) Consider the first function.

`f(x)=-2x+1`

If x = -1, then we get,

`\begin{gathered} f(-1)=-2(-1)+1 \\ =2+1=3 \end{gathered}`

So, the point (-1, 3) satisfies the first function.

If x = 0, then we get,

`\begin{gathered} f(0)=-2(0)+1 \\ =1 \end{gathered}`

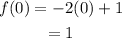
So, the point (0, 1) also satisfies the first function.

Therefore, (-1, 3) and (0, 1) satisfies the first function.

b) Next, let us consider the second function.

`f(x)=-2x^2-4x+1`

If x = -1, then we get,

`\begin{gathered} f(-1)=-2(-1)^2-4(-1)+1 \\ =-2+4+1 \\ =3 \end{gathered}`

So, the point (-1, 3) satisfies the second function.

If x = -2, then we get,

`\begin{gathered} f(-2)=-2(-2)^2-4(-2)+1 \\ =-8+8+1 \\ =1 \end{gathered}`

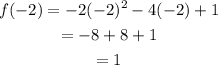
So, the point (-2, 1) satisfies the second function.

If x = 0, then we get,

`\begin{gathered} f(0)=-2(0)^2-4(0)+1 \\ =1 \end{gathered}`

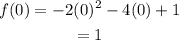
So, the point (0, 1) also satisfies the second function.

Therefore, (-1, 3), (-2, 1) and (0, 1) satisfies the second function.

c) Next let us consider the third function.

`f(x)=2√(x+2)+1`

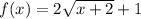
If x = -1, then we get,

`\begin{gathered} f(-1)=2√(-1+2)+1 \\ =2+1 \\ =3 \end{gathered}`

So, the point (-1, 3) satisfies the third function.

If x = 2, then we get,

`\begin{gathered} f(2)=2√(2+2)+1 \\ =2√(4)+1 \\ =2(2)+1 \\ =5 \end{gathered}`

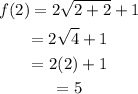
So, point (2, 5) satisfies the third function.

If x = -2, then we get,

`\begin{gathered} f(-2)=2√(-2+2)+1 \\ =0+1 \\ =1 \end{gathered}`

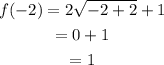
So, the point (-2, 1) satisfies the third function.

Therefore, (-1, 3), (-2, 1) and (2, 5) satisfies the third function.

Final answer:

• The first function is mapped to the points

`\left(-1,3\right)\text{ }and\text{ }(0,1)`

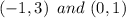
• The second function is mapped to the points

`\left(-1,3\right),(-2,1)\text{ }and\text{ }(0,1)`

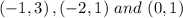
• The third function is mapped to the points

`\left(-1,3\right),(-2,1)\text{ }and\text{ }(2,5)`