The compound interest formula for the amount of money A in an account after t years if a principal P is invested at an annual interest rate r (written as a decimal) which is compounded n times a year, is:

In this case, the interest rate of 3.4% (0.034), the amount after 13 years, $24,155.71 and the number of compounding periods a year, 2, are given. The principal P is unknown.
Then, isolate P from the equation:
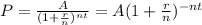
Replace A=24,155.71, r=0.034, n=2 and t=13 to find the principal P that Sophie deposited at the beginning:

Therefore, to the nearest whole number, the amount that Sophie deposited was $15,584.