We start by graphing the vertices of the triangle:
The first transformation is a translation 4 units to the right and 3 units up.
Then, we will get:
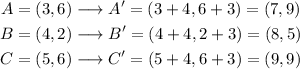
The rule applied for this translation is:
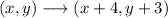
Now we have to reflect the points across the vertical line x=1. Only the horizontal coordinates will change, while the vertical coordinates remain equal.
This transformation has the rule:
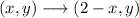
Then, we will have:
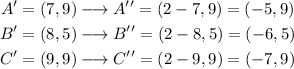
Now we can graph the image and the pre-image: