Answer:
D. 5x - 3y = 27
Step-by-step explanation:
Definition: Two lines are perpendicular if the product of their slopes is -1.
Given the line: y=- 3/5x + 1
Slope = -3/5
Therefore, the slope of the perpendicular line must be = 5/3.
To determine the perpendicular line, we make y the subject in each equation.
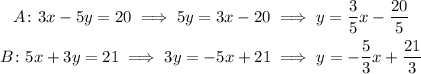
We do likewise for options C and D.

We can see that option D has a slope of 5/3.
It is the line perpendicular to the line y = - 3/5x + 1.