Question

the force needed to keep a car from skidding on a curve varies jointly as the weight of the car and the square of its speed and inversely as the radius of the curve. It takes 2,600 lbs of force to keep a 1,800 lb car from skidding on a curve with a radius of 425 ft at 45 mph. What force (in lbs) is needed to keep the same car from skidding when it takes a similar curve with a radius of 450 ft at 55 mph? round to the nearest 10 lbs. _____ lb

Answer 1

3670 lb.

Step-by-step explanation:

If we measure the force in pounds, distance in ft and time in hours, then the force need to keep the car from skidding is given by

`F=k(wv^2)/(R)`

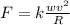
where k is a constant, w = weight, R = radius of the path, and v = velocity of the car.

Now we know that when v = 45 mph, w = 1800 lb, R = 425, and F = 2600 lb; therefore,

`2600=k(1800\cdot(45)^2)/(425)`

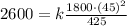
and we need to solve for k.

simplifying the above gives

`2600=k(8576.4705.\mathrm{})`

solving for k gives

`\boxed{k=(221)/(729)}`

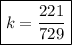
Now that we have the value of k, we can find the force needed for

There seemes to be a technical issue with the answer tab. So I wont be able to complete the explanation. But you can find the force by F = (221/729)*(1800*(55^2))/450.