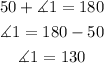The first step is to find the value of x. The sum of angles (2x+10) and (3x-5) is 180 because they are consecutive interior angles
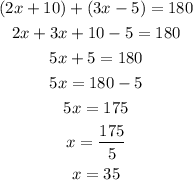
Now, you can find the measure of 3 of the angles
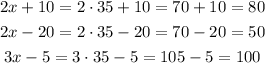
The sum of 2x-20 and angle 1 is 180 because they are consecutive interior angles, use this to find angle 1 measurement