In order to find if the student is correct or not, let's analyze the formula for the area of a circular sector:
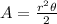
Where r is the radius and theta is the central angle.
If the radius is doubled, since it is squared, the area will be multiplied by 4 instead of being doubled as well:
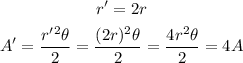
Therefore we disagree with the student.