Question

need help with example #12 state the number of possible triangles that can be formed using the given measurements

Answer 1

To solve this question, follow the steps below.

Step 01: Use the law of sines to find m∠C.

According to the law of sines:

`(a)/(sin(A))=(b)/(sin(B))=(c)/(sin(C))`

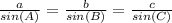
Then, let's compare A and C:

`(a)/(sin(A))=(c)/(sin(C))`

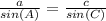
Step 02: Substitute the values and find m∠C.

a = 35 m

b = 23 m

m∠A = 152°

`\begin{gathered} (35)/(sin(152))=(23)/(sin(C)) \\ Multiplying\text{ }both\text{ }sides\text{ }by\text{ }sin(C)\text{ } \\ (35)/(sin(152))sin(C)=(23)/(sin(C))*sin(C) \\ (35)/(sin(152))sin(C)=23 \\ Mult\imaginaryI ply\imaginaryI ng\text{ }both\text{ }sides\text{ }by\text{ }(sin(152))/(35) \\ sin(C)(35)/(sin(152))*(sin(152))/(35)=23*(s\imaginaryI n(152))/(35) \\ sin(C)=23*\frac{s\mathrm{i}n(152)}{35} \\ sin(C)=0.3085 \\ sin^(-1)(0.3085)=C \\ C=17.96 \\ or \\ C=180-17.96 \\ C=162.03 \end{gathered}`

Step 03: Evaluate the results.

Since the sum of the angles of a triangle is 180°, the sum of m∠A and C must be lower than 180°.

So, 152 + 17.96 < 180°

152 + 162.03 > 180°

Then, the only possibility is m∠C = 17.96°

If you want to find m∠B, use the sum = 180°.

m∠A + m∠B + m∠C = 180

m∠B = 180 - m∠A - m∠C

m∠B = 180 - 152 - 17.96

m∠B = 10.04°

Then, only one triangle can be formed using the given measurements.

Answer: One.