Question

Scenario: You are an employee of the Dupont Chemical Industry working with a team off 3-4 chemists. The laboratory division for which you work for focuses on the synthesis of ammonia (NH3) from hydrogen and nitrogen. (This reaction is commonly referred to as the Haber Process) Your supervisor has informed your group that he needs you to produce at least 125 grams of ammonia by the end of the day or else your division will be shut down. When checking your supplies you realize that you have exactly 100 grams of nitrogen and 30 grams of hydrogen gas. Will your group still be employed at the end of the day? Show all dimensional analysis steps that are necessary to this problem. What is the maximum amount of ammonia that can be made given your supplies?

Answer 1

Firstly, we need to write the equation for the process.

We start with hydrogen gas, H₂, and nitrpgen gas, N₂, and end with NH₃, so the unbalanced reaction is:

`H_2+N_2=NH_3`

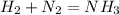
To balance it, we can add a coefficient of 2 to NH₃ so that N gets balanced and then we will need to add a coefficient of 3 to H₂ so H gets balanced:

`3H_2+N_2=2NH_3`

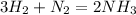
With the balanced reaction, we will need the molar mass of each component, which we can calculate using the molar masses of the atoms H and N:

`\begin{gathered} M_(H_2)=2\cdot M_H=2\cdot1.00794g\/mol=2.01588g\/mol \\ M_(N_2)=2\cdot M_N=2\cdot14.0067g\/mol=28.0134g\/mol \\ M_(NH_3)=1\cdot M_N+3\cdot M_H=1\cdot14.0067g\/mol+3\cdot1.00794g\/mol=17.03052g\/mol \end{gathered}`

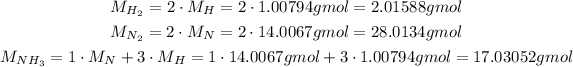
Now, we need to convert the masses of nitrogen gas and hydrogen gas to number of moles:

`\begin{gathered} M_{H_(2)}=\frac{m_(H_2)}{n_{H_(2)}} \\ n_(H_2)=\frac{m_(H_2)}{M_{H_(2)}}=(30g)/(2.01588g\/mol)=14.8818\ldots mol \end{gathered}`
`\begin{gathered} M_{N_(2)}=\frac{m_(N_2)}{n_{N_(2)}} \\ n_(N_2)=\frac{m_(N_2)}{M_{N_(2)}}=(100g)/(28.0134g\/mol)=3.5697\ldots mol \end{gathered}`

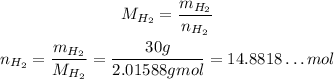
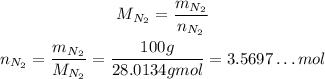
Now, we need to find which of the two is the limiting reactant, that is, which we have less considering the ratio they react.

Each 1 mol of N₂ that react will need 3 mol of H₂, so if all the 3.5697... mol of N₂ react, than we will need

`3\cdot3.5697\ldots mol=10.7091\ldots mol`

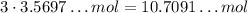
10.7091... mol of H₂. Since we have 14.8818 mol of H₂, we have excess of H₂, which means that N₂ is the limiting reactant.

Since H₂ is the limiting reactant, the most that we can produce of NH₃ is the corresponding of 3.5697... mol of reacting N₂.

From the equation again, we can see that each mol of N₂ that reacts will produce 2 mol of NH₃, so if all the limiting 3.5697... mol react, we will get:

`2\cdot3.5697\ldots mol=7.1394\ldots mol`

7.1397... mol of NH₃, so this is the maximum number of moles we can get of NH₃:

`n_{NH_(3)}`

Using the molar mass of NH₃, we can convert this to mass:

`\begin{gathered} M_{NH_(3)}=\frac{m_(NH_3)}{n_{NH_(3)}} \\ m_(NH_3)=n_(NH_3)\cdot M_(NH_3)=7.1394\ldots mol\cdot17.03052g\/mol=121.58\ldots g\approx121g \end{gathered}`

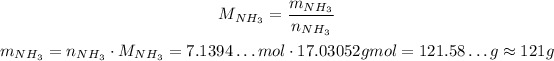
So, the maximum mass of NH₃ you can produce with the given masses of reactant is 121 grams, which is not enough for whats has been asked.