Given:
$200 - payment for the self-proclaimed psychic
$1.50 - club's earnings for each ticket
Find: club's gain/lose after selling 100 tickets and number of tickets in order to break-even
Solution:
Since x = represents the number of tickets sold, we can say that the profit of the club is y = ($1.50 times the number of tickets x sold) - the payment for the psychic.
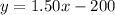
a. Let's plugin x = 100 tickets in the formula above.
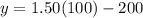
Then, solve.
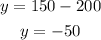
Since the answer is negative, by selling 100 tickets, the club loses $50.
b. Break-even means there is no gain nor lose. Hence, the charge and the earnings of the club are equal. So, with this, we will assume that y = 0.
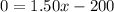
Then, we can solve for x or the number of tickets needed.
Add 200 on both sides of the equation.
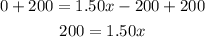
Divide both sides by 1.50.
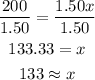
Hence, the club needs to sell 133 tickets in order to break even.