Question

From the top of an offshore oil rig that is 149 ft. above sealevel, the angle of depression of a passing ship is 23°. Findthe distance between the ship and the top of the oil rig.Round your answer to the nearest tenth.Distance= ft

Answer 1

First let's ilustrate this problem with the following triangle:

So, in order to calculate the distance x, first let's calculate the angle y, which is complementary to the angle 23°:

`\begin{gathered} 23+y=90 \\ y=90-23 \\ y=67\degree \end{gathered}`

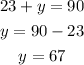
Then, to find the distance x, we can use the cosine relation of angle y.

The cosine is defined as the length of the adjacent side to the angle over the hypotenuse of the triangle. So we have:

`\begin{gathered} \cos (67\degree)=(149)/(x) \\ 0.3907=(149)/(x) \\ x=(149)/(0.3907) \\ x=381.37\text{ ft} \end{gathered}`

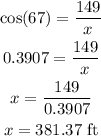
Rounding to the nearest tenth, we have that the distance between the top of the oil rig and the ship is 381.4 ft.