To solve the exercise we can first find the equation of a line perpendicular to the given lines.
Two lines are parallel if their lines are equal.
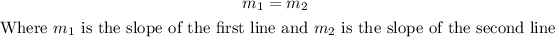
And two lines are perpendicular if their respective slopes have the following relationship:
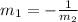
Then, the slope of the line perpendicular to the given lines is:

Now, let us find a point through which the second line passes:
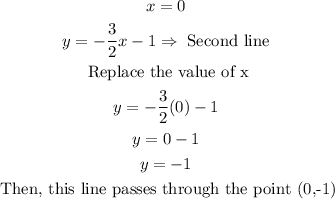
Now, using the point-slope formula we can find the equation of the line perpendicular to the given parallel lines:
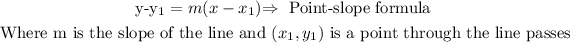

Now, we can find the point where the first line and the line that is perpendicular to the two given lines meet:

Now, we can plug the value of x into the equation of the first line to find its respective y-coordinate:
![undefined]()