Question

Could you help me understand how to solve systems of equations and functions I do not under stand how to do it

Answer 1

Step-by-step explanation

Suppose that we have the following system of equations:

(1) x + 2y = 30

(2) 3x + y = 14

The key is to isolate one variable from one equation and substitute into another in order to get the first solution:

We can first isolate x from (1) by subtracting -2y to both sides:

x + 2y - 2y = 30 - 2y

Simplifying:

x = 30 - 2y

Plugging in x = 30 - 2y into the second equation:

`3(30-2y)+y=14`

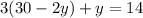
Applying the distributive property:

`90-6y+y=14`

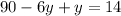
Adding like terms:

`90-5y=14`

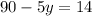
Subtracting -90 to both sides:

`-5y\text{ = 14 - 90}`

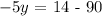
Dividing both sides by -5:

`y=(14-90)/(-5)`

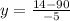
Subtracting numbers:

`y=(-76)/(-5)`

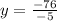
Simplifying:

`y=(76)/(5)`

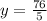
Now, plugging in y=76/5 into the first equation:

`x+2\cdot(76)/(5)=30`

Multiplying numbers:

`x+(152)/(5)=30`

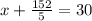
Subtracting -152/5 to both sides:

`x=30-(152)/(5)`

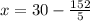
Subtracting numbers:

`x=-(2)/(5)`

In conclusio, the solution to the system of equation is:

x=-2/5, y=76/5