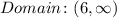1 Answer

Tohster · Answer 1 · 2023-12-01T11:29:04+0000

Given the graph of a Piecewise Function, you can identify that it has three pieces. See the picture below:

By definition, the open circles indicates that that endpoint is not included in the interval of the function.

By definition, the Domain of a function is the set of all the input values (x-values) for which the function is defined.

In this case, you need to analyze each piece in order to determine its Domain:

1. Notice that piece 1 goes from:

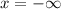
$x=-\infty$

To:

But -2 is not included. Therefore:

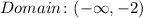
$Domain\colon(-\infty,-2)_{}$

2. Notice that piece 2 goes from:

To:

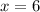
But since its endpoints are not included:

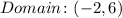
$Domain\colon(-2,6)_{}$

3. Piece 3 goes from:

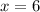
To:

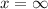
$x=\infty$

Since the x-value 6 is not included:

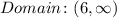
$Domain\colon(6,\infty)_{}$

Hence, the answer is:

- For the first piece from left to right:

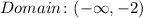
$Domain\colon(-\infty,-2)_{}$

- For the middle piece:

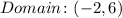
$Domain\colon(-2,6)_{}$

- For the third piece from left to right:

$Domain\colon(6,\infty)_{}$

Please log in or register to add a comment.