Question

i have the information for the questions Part 1)Group of items - A basket of fruitsCharacteristics of interest - Type of fruitPossible outcomes - Oranges = 0.4 Mangos = 0.6Number of items - A basket with twenty fruitsAction - A fruit is selected from the basket randomly without replacementPart 2)Since a dice has 6 sides representece the probability is shown 1 2 3 4 5 616.6 16.6 16.6 16.6 16.6 16.67% 7% 7% 7% 7% 7%Each side has a 16.67% equal chance of being selected.Part 3)Experiment 1:P(M)=6/10Probabilty of Oranges = 0.6P(A)=4/10Probabilty of Oranges = 0.40.6+0.4=1Hence verifield

Answer 1

The experiment consists of picking a piece of fruit without replacement from a basket.

The probabilities are

`\begin{gathered} P(Mango)=P(M)=0.6 \\ and \\ P(Orange)=P(O)=0.4 \end{gathered}`

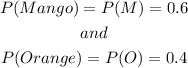
The experiment clearly cannot be repeated 5000 times if the basket only has 20 fruits.

Using theoretical probability,

`\begin{gathered} 5000*P(Mango)=3000 \\ 5000*P(O)=2000 \end{gathered}`

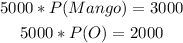
Theoretically, we would obtain 3000 mangoes and 2000 oranges if the experiment is repeated 5000 times.

The provided information implies that the experimental probability is the same as the theoretical probability, in this instance.

To use the expected value, one would need to assign a numerical value to 'mango' and to 'orange'; then, use the expected value formula.