Question

A beam of radiation is to be used to treat a tumor known to be 5.7 cm beneath thepatient's skin. To avoid damaging a vital organ, the radiologist moves the radiationsource over 8.3 cm. At what angle (nearest degree) must the radiologist aim the radiationsource to hit the tumor?

Answer 1

Step-by-step explanation:

Let's redraw the diagram first.

To determine the missing angle, we can use the tangent function.

`\theta=tan^(-1)\frac{opposite\text{ }side\text{ }of\text{ }the\text{ }angle}{adjacent\text{ }side\text{ }of\text{ }the\text{ }angle}`

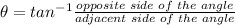
In the diagram, the opposite side of the angle is the depth of the tumor under the skin surface which is 5.7 cm. The adjacent side of the angle is the horizontal distance on the surface of the skin from the tumor which is 8.3 cm.

Let's plug in these values to the function above.

`\theta=tan^(-1)(5.7cm)/(8.3cm)`

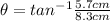
Evaluate the expression using a calculator.

`\begin{gathered} \theta=tan^(-1)(0.686746988) \\ \theta=34.479\approx34\degree \end{gathered}`

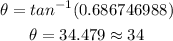
Answer:

Therefore, the radiologist must aim the radiation source at approximately 34º to hit the tumor and avoid damaging the vital organ.